Leetcode-70 爬楼梯

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2 输出：2 解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶示例 2：

输入：n = 3 输出：3 解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

提示： 1 <= n <= 45

递归实现

每层楼梯均要做一下判断：

爬 1 级：此时问题变为爬 n-1 级楼梯有多少不同方法
爬 2 级：此时问题变为爬 n-2 级楼梯有多少不同方法

因此爬 n 级台阶的方法数量 = (爬 n-1 级台阶的方法数量) + (爬 n-2 级台阶的方法数量)

1
2
3
4
5
6
7


func climbStairsRecursion(n int) int {
    // 递归边界
	if n <= 1 {
		return 1
	}
	return climbStairsRecursion(n-1) + climbStairsRecursion(n-2)
}

递归 + 记忆化

在计算爬 n-1 和 n-2 级楼梯需要的方法数量时，会存在大量重复计算，因此可以使用 map 或者数组来记录已计算的数据来进行复用

由于楼梯台阶数是一个有序排列的数组，因此可以数组来进行记录

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


func climbStairsRecursionMemory(n int) int {
	var m = make([]int, n+1)
	var dfs func(int) int
	dfs = func(n int) int {
		if n <= 1 {
			return 1
		}
		if m[n] == 0 {
			m[n] = dfs(n-1) + dfs(n-2)
		}
		return m[n]
	}
	return dfs(n)
}

自底向上递推

在之前的解决方案中我们已经利用了 f(n) = f(n-1) + f(n-2) 的关系式，并通过递归将由 n 逐渐分解为更小的计算单元。

但是在过程中存在大量的函数调用和中间状态存储，因此我们可以考虑从最小的台阶开始计算，依次向上计算到 n。

如下图：

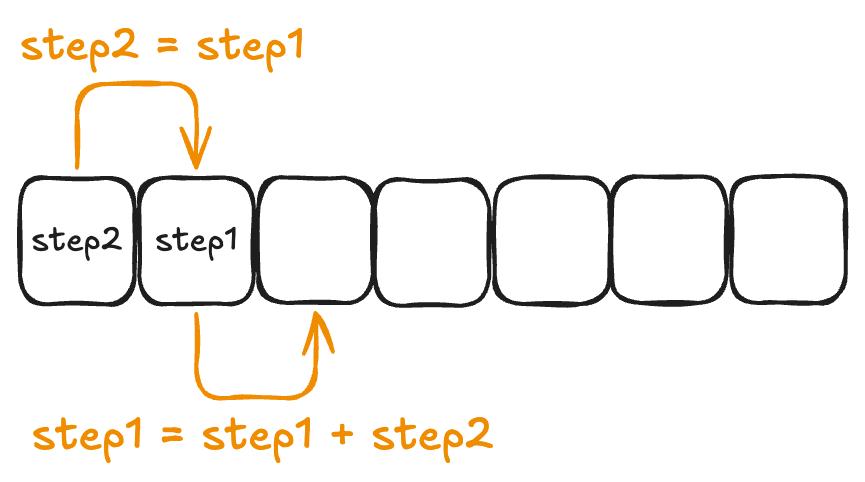
实现代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


func climbStairs(n int) int {
   var (
      step1 = 1 // 对应递归的 n-1
      step2 = 1 // 对应递归的 n-2
   )
   for i := 2; i <= n; i++ {
	   step2, step1 = step1, step1+step2
   }
   return step1
}